A schedule and list of abstracts can be found below. You can also download a PDF with the schedule and a brief program for printing. You will also find some material below (posters and PDF slides).
Index of abstracts
Abstracts for the courses
Diogo Gomes
Pierre-Emmanuel Jabin
James Norris
Mark Peletier
Abstracts for the talks
Maria Bruna
José A. Carrillo
Young-Pil Choi
Amit Einav
Susana Gutiérrez
Yanghong Huang
Juan J. L. Velázquez
Johannes Zimmer
Abstracts for the posters
Giovanni Bonaschi
Rafał Celiński
Helge Dietert
Joep Evers
Simone Fagioli
Tom Holding
Thomas de Jong
Mitchell Kovacic
Oxana Manita
Alpár Richárd Mészáros
Patrick van Meurs
Marco Morandotti
Christian Nessler
Edgard Pimentel
Torsten Trimborn
Roberto M. Velho
Kit Yates
Mattia Zanella
Gleb Zhelezov
Schedule
| Monday | Tuesday | Wednesday | Thursday | Friday | |
| 9:15 - 10:05 | 9:15 Registration 9:45 Opening |
Peletier | Gomes | Huang | Norris |
| 10:15 - 11:05 | Jabin | Jabin | Jabin | Gomes | Gutiérrez |
| 11:05 - 11:30 | Coffee break | Coffee break | Coffee break | Coffee break | Coffee break |
| 11:30 - 12:20 | Peletier | Gomes | Norris | Norris | Zimmer |
| 12:20 - 14:15 | |||||
| 14:15 - 15:05 | Gomes | Jabin | Carrillo | Einav | |
| 15:05 - 15:30 | Coffee break | Coffee break | Coffee break | Coffee break | |
| 15:30 - 16:20 | Bruna | Velázquez | Choi | Peletier | |
| 16:30 - 17:20 | Poster session | ||||
| Evening |
Abstracts for the courses
Introduction to the regularity theory for mean-field games
In this course we will cover various aspects of the regularity theory for mean-field games. We will start with a brief introduction to Hamilton-Jacobi equations and viscosity solutions. Then we present several techniques to obtain regularity for Hamilton-Jacobi equations and Fokker-Planck equations. In addition to maximum principle and energy type estimates, we will introduce more recent tools such as the non-linear adjoint method. Then we derive a number of a-priori estimates for stationary and time-dependent mean-field games. Finally, gathering the previous results we establish existence of smooth solutions for various classes of mean-field games.
Mean field limit for systems of many particles
I will present the main results concerning the derivation of the mean field limit for systems of many particles with so-called long range interactions.
We will start with the classical techniques, introduced in the 70's by Braun and Hepp, Dobrushin and others, for Lipschitz interaction kernels. We will then study the singular cases for macroscopic limits, i.e. starting with systems of ODE's of order 1. In that case the derivations are now rather well understood following the works of Goodman, Hou and Lowengrub, Schochet and more recently Hauray. Finally I will present some of the main remaining challenges for ODE's of order 2, such as in classical Newton mechanics.

Fluid limits for some mean-field particle systems
PDF slides for J. Norris' third lecture are available here.
- Lecture 1: Fluid limits for Markov chains
- Lecture 2: Marcus-Lushnikov process
- Lecture 3: Kac process
The following articles address similar themes.
- Darling, R. W. R.; Norris, J. R. Differential equation approximations for Markov chains. Probab. Surv. 5 (2008), 37--79. Preprint arXiv:0710:3269
- Norris, James R. Smoluchowski's coagulation equation: uniqueness, non-uniqueness and a hydrodynamic limit for the stochastic coalescent. Ann. Appl. Probab. 9 (1999), no. 1, 78--109.
From Diffusion to Reaction via Gamma-convergence
Since Arrhenius, Wigner, and Kramers, we understand chemical reactions as an `activated process': we think of the system as a point moving in an energy landscape, sliding down the energy slopes while being jiggled by thermal noise. The energy wells correspond to stable chemical species, and a reaction is a motion from one well to another. The mountain-pass connections between wells represent high-probability reaction paths.
In 1940 Kramers gave the first quantitative predictions of reaction rates based on this picture, and his name is still associated with the formula. In these three talks I want to revisit one of his calculations, the high-activation limit, and frame it in modern mathematical language so that we can then prove it rigorously. As part of this work we will generalize existing results on convergence of linear semigroups to cases where the limiting problem is degenerate.
The tools will be those of variational calculus and differential equations, but not much will be required as prior knowledge of either.
Reference: Peletier, Savaré, and Veneroni, From Diffusion to Reaction via Gamma-convergence, SIAM J. Math. Anal. 42, pp. 1805-1825.
Abstracts for the talks
Finite-size effects in diffusion

When diffusing agents interact with each other their motions are correlated, and the configuration space is of very high dimension. Often an equation for the marginal distribution function of one particle (the "concentration") is sought by "integrating out" the positions of all the others. This leads to the classic problem of closure, since the equation for the concentration so derived depends on the two-point correlation function. A common closure is to assume independence at this stage, leading to some form of nonlinear diffusion equation. Such an approach works well for long-range interactions, but fails for short-range interactions.
Here we consider an alternative approach using matched asymptotic expansions, in which the approximation is entirely systematic, and no closure is needed. We show how this approach works for a system of finite-sized particles and compare the result with numerical simulations of the stochastic particle system.
Minimizers of Interaction Energies
I will start by reviewing some recent results on qualitative properties of local minimizers of the interaction energie to motivate the main topic of my talk: to discuss global minimizers. We will show the existence of compactly supported global miminizers under quite mild assumptions on the potential in the complementary set of classical H-stability in statistical mechanics. A strong connection with the classical obstacle problem appears very useful when the singularity is strong enough at zero. An approach from discrete to continuum is also quite nice under convexity assumptions on the potential.
This is based on three preprints/works in preparation one together with F. Patacchini, J.A. Cañizo, another one with M. Delgadino and A. Mellet, and finally with M. Chipot and Y. Huang.
Mean-field limit and propagation of chaos for aggregation equations

In this talk, we discuss the mean-field limit of large ensembles of interacting particles with applications in swarming models. We show how to use related techniques from fluid mechanics equations applied to first order models for swarming, also called the aggregation equations. We give qualitative bounds on the approximation of initial data by particles to obtain the mean-field limit for radial singular (at the origin) potentials up to the Newtonian singularity. We also show the propagation of chaos for more restricted set of singular potentials.
Joint work with: José A. Carrillo (Department of Mathematics, Imperial College London) and Maxime Hauray (Centre De Mathématiques et Informatique, Université D'Aix-Marseille, Technopôle Château-Gombert).
Of Chaos and Chaotic States in Kac's Model

One of the most influential equations in the kinetic theory of gases is the so-called Boltzmann equation, describing the time evolution of the probability density of a particle in dilute gas. The problem of proving its validity is an important, and significant, problem in the field of Kinetic Theory.
In 1956 Marc Kac presented an attempt to solve a simple case of this problem by showing how the spatially homogeneous Boltzmann equation can arise as a mean field limit of a model of many particles. He considered a stochastic linear model of \(N\) indistinguishable particles with one-dimensional velocities, that undergo a random binary collision process. Under the property of 'chaoticity' Kac managed to show that when one takes the number of particles to infinity, the limit of the first marginal of the N-particle probability density function satisfies a caricature of the Boltzmann equation, the so-called Boltzmann-Kac equation.
The concept of chaoticity, and that of propagation of chaos, has become a fundamental one in many other models of systems of many objects. As such, there is much interest in identifying chaotic states, as well as the more robust states we call 'entropically chaotic'. In our talk we will shortly present Kac's model, and explain it connection to the Boltzmann equation. We will then discuss a particular, intuitive, type of chaotic, and even entropically chaotic, family — one that is generated by a known one-particle function. We will see how local central limit theorems play an essential role in proving that the states are indeed chaotic, and present a new Levy type local central limit theorem that allowed us to extend previous results.
On estimates for kinetic equations and applications to models of chemotaxis
We begin recalling the well-known dispersive and Strichartz estimates for the kinetic transport equation. Special emphasis will be given to mentioning the latest results in this setting.
The aim of the rest of this talk is to see an application of these
estimates to study certain kinetic models of chemotaxis. Chemotaxis is
a process in which bacteria/cells change their state of movement due
to the presence of chemoattract in the substrate. At the microscopic
level chemotaxis is modelled by a nonlinear kinetic transport equation
with a quadratic nonlinearity coupled to a parabolic-elliptic equation
for the concentration of chemoattractant. We will discuss the
existence of weak solution to several models of chemotaxis using
dispersion and Strichartz estimates. Several open problems will be
also mentioned.

Stability of self-propelled particle systems and existence of flocking solutions for the continuum limit
Complex behaviours of animal swarming such as fish schools and bird flocks exhibit macroscopic patterns from interactions between individuals. These phenomena can be modelled both by agent-based particle systems and their continuum limiting PDEs, providing a mathematical framework frequently used in crowd dynamics, opinion formation and cell biology. In this talk, I will discuss a self-propelled particle systems for concurrent moving flocks and rotating mills, with simple attractive-repulsive interactions. At the particle level, the stability of the flocks is shown to be implied from the corresponding first order system. In the continuum limit, in the special case of Quasi-Morse potential, the density of the flock can be obtained. The flock solution exist only in the parameter regime where the potential is not H-stable, the same condition confirmed numerically for the particle systems. This is a joint work with José Carrillo and Stephan Martin.
Singularity formation for kinetic equations with cubic nonlinearities
In this talk I will discuss some recent results concerning the formation of singularities for two particular kinetic equations, namely Nordheim's equation for bosons and the Weak Turbulence kinetic equation associated to the Nonlinear Schrödinger Equation. The solutions of these equations can yield singularity formation in finite time for homogeneous particle distributions. This singular behaviour is seemingly related to the formation of Bose-Einstein condensates. Issues like the long time asymptotics for the solutions of the Weak Turbulence Equation will be also discussed. (joint work with M. Escobedo).
Entropic flows, stochastic perturbations and microscopic models
As starting point, different ways to link some PDEs of diffusive type to particle models will be reviewed. Typically, the PDE will be related to a minimisation problem of a large deviation rate function from probability.
The underlying microscopic process contains more information, notably fluctuations around the minimum state described by the deterministic PDE. Can stochastic terms be derived which model this additional information, in a way that is compatible to the limit passage via large deviations (and the geometric structure, such as the Wasserstein setting)? This question will be investigated for linear diffusion, and existence of a corresponding (nonlinear stochastic) equation will be discussed and analysed.
This is joint work with Rob Jack and Shangjiang Guo.
Abstracts for the posters
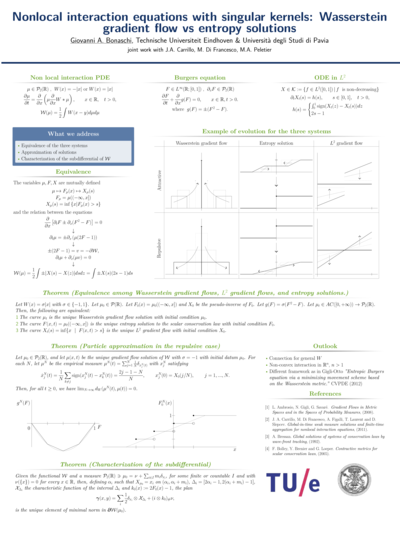
Nonlocal interaction equations with singular kernels: Wasserstein gradient flow vs entropy solutions
An arXiv preprint of a paper related to the content of this poster is available here: "Equivalence of gradient flows and entropy solutions for singular nonlocal interaction equations in 1D"
We prove the equivalence between the notion of Wasserstein gradient flow for a onedimensional nonlocal transport PDE with attractive/repulsive Newtonian potential on one side, and the notion of entropy solution of a Burgers-type scalar conservation law on the other. The solution of the former is obtained by spatially differentiating the solution of the latter. The proof uses an intermediate step, namely the \(L^2\) gradient flow of the pseudo-inverse distribution function of the gradient flow solution. We use this equivalence to provide a rigorous particle-system approximation to the Wasserstein gradient flow, avoiding the regularization effect due to the singularity in the repulsive kernel. The abstract particle method relies on the so-called wave-front-tracking algorithm for scalar conservation laws. Finally, we provide a characterization of the sub-differential of the functional involved in the Wasserstein gradient flow.
Asymptotic behaviour to the model of chemotactic E. Coli colonies
We consider the following initial-boundary value problem \begin{align} \label{eq1} &u_t= \Delta u-\nabla\cdot(u\nabla c)+g(u)nu-b(n)u\\ \label{eq2} &c_t=d_c\Delta c+\alpha u-\beta c\\ \label{eq3} &n_t=d_n\Delta n-\gamma g(u)nu\\ \label{eq4} &w_t= b(n)u, \end{align} where \(x\in\Omega\subset\mathbb{R}^d,\ t>0\) and with supplemented the Neumann boundary conditions i.e \begin{align} \label{bound_cond} \frac{\partial u}{\partial \nu}=\frac{\partial c}{\partial \nu}=\frac{\partial n}{\partial \nu}=0 \end{align} for \(x\in\partial\Omega\), \(t>0\) and nonnegative initial data \[\begin{equation} \begin{split} &u(x,0)=u_0(x), \quad c(x,0)=c_0(x), \\ &n(x,0)=n_0(x), \quad w(x,0)=w_0(x). \label{eq-ini} \end{split} \end{equation}\]
Budrene and Berg [2,3] observed in experiments that a chemotactic strain of {\it Escherichia coli} generate complex and ordered patterns. Recently, Mimura and his group proposed the system of four coupled partial differential equations \eqref{eq1}-\eqref{eq4} and suggested by numerical simulation that the resulting patterns are possibly generated in a self-organized way. However, there is still little done in the rigorous study so far.
I will present new results concerning the asymptotic behaviour of solutions to \eqref{eq1}-\eqref{eq-ini}, under some general assumptions on functions \(g\), \(b\) and \(\chi\). First, I will show some basic properties of solutions such as: local-in-time existence, positiveness, boundedness of mass (integral of \(u\)) and asymptotic behaviour of space homogenous solution as well as corresponding masses.
Next, we will consider the one-dimensional case and prove that solutions exist globally-in time and, for large values of time, they behave similarly to the space homogenous solution.
Later on, we will prove that, in higher dimensions, we have global-in-time existence of solutions for sufficiently small initial conditions. Moreover, we show that those solutions has the same asymptotics as in the one-dimensional case.
Finally, we will show that if we change the equation \eqref{eq2} for elliptic one and consider \(\chi(c)=c\) then, for sufficiently large initial mass, solutions may blow-up in finite time.
References
- A. Aotani, M. Mimura, T. Mollee, A model aided understanding of spot pattern formation in chemotactic E. coli colonies, Japan J. Indust. Appl. Math. 27 (2010), pp. 5-22.
- E. O. Budrene, H. Berg, Complex patterns formed by motile cells of Escherichia coli, Nature 349 (1991), pp. 630-633.
- E. O. Budrene, H. Berg, Dynamics of formation of symmetrical patterns by chemotactic bacteria, Nature 376 (1995), pp. 49-53.
- P. P. Htoo, M. Mimura, I. Takagi, Global solutions to a one-dimensional nonlinear parabolic system modeling colonial formation by chemotactic bacteria., Adv. Stud. Pure Math. 47 (2007), pp. 613-622.

Characterisation of gradient flows on finite state Markov chains
The seminal paper of Jordan, Kinderlehrer, and Otto (1998)
identified Markov processes in the continuous setting as gradient
flows of the entropy using the Wasserstein distance. In the discrete
setting, Maas (2011) showed that the Wasserstein distance does not
allow the identification of the heat flow as a gradient flow. With the
assumption of time-reversibility, he constructed a metric on the space
of probability measures such that the heat heat flow becomes the
gradient flow of the relative entropy. We prove that the
time-reversibility is also necessary, so that time-reversibility can
be characterised by the existence of such a metric. When we allow a
more general functional in place of the relative entropy, we show that
the necessary and sufficient condition becomes that the transition
matrix is real-diagonalisable. Finally, we discuss what aspects of the
functional are uniquely determinned by the Markov chain.

Boundary conditions for measure-valued evolutions
(Joep Evers, Adrian Muntean & Sander Hille)
This poster deals with imposing a flux boundary condition on a
non-conservative measure-valued mass evolution problem posed on a
bounded interval. We start from a thin layer near the boundary in
which absorption of mass takes place, and let the width of this layer
tend to zero. We derive the convergence rate for the approximation
procedure as well as the structure of the flux boundary condition in
the limit problem.

Nonlocal interaction equations with two species
We present a systematic existence and uniqueness theory of weak measure solutions for systems of nonlocal interaction PDEs with two species, which are the PDE counterpart of systems of deterministic interacting particles with two species. The main motivations behind those models arise in cell biology, pedestrian movements, and opinion formation. In case of symmetrizable systems (i.e. with cross-interaction potentials one multiple of the other), we provide a complete existence and uniqueness theory within (a suitable generalization of) the Wasserstein gradient flow theory, which allows to consider interaction potentials with discontinuous gradient at the origin. In the general case of non symmetrizable systems, we provide an existence result for measure solutions which uses a implicit-explicit version of the JKO scheme, which holds in a reasonable non-smooth setting for the interaction potentials. Uniqueness in the non symmetrizable case is proven for smooth potentials using a variant of the method of characteristics. One-dimensional local nonlinear stability for a nonlocal predator-prey model is discussed, both at particles and PDE levels providing some numerical results.
Mean field models of neuron clusters
The past decade has seen the introduction of a variety of kinetic mean- field equations describing the statistical behaviour of neuronal networks [Cai et al., 2006]. We consider conductance/voltage LIF (Leaky Integrate and Fire) models and the corresponding kinetic equations describing the mean field limits. These models have better dynamical properties, and are closer to the biology, compared to the pure voltage LIF models which have been the main focus of previous study. However, mathematical hurdles have until now prevented the development of any rigorous theory. We present a new approach using Wasserstein metrics on \(P(P(\mathbb{R}) \times \mathbb{R}_+ )\) which allows us to establish both existence, uniqueness and the mean-field limit. The approach is flexible enough to encompass many different input spikes models and the addition of noise. Interestingly, our limiting equation differs slightly in form from that [Cai et al., 2006].
References
[1] David Cai, Louis Tao, Aaditya V. Rangan, and David W. McLaughlin. Kinetic theory for neuronal network dynamics. Communications in Mathematical Sciences, 4(1):97–127, 03 2006.
Modelling fungal hyphae growth by extending the thin viscous sheet equations
The cell growth of fungal hyphae typically proceeds as an elongating expansion in a single direction. It grows at a constant speed preserving the overall tube- like form. Hence from a mathematical viewpoint the growth can be described by a travelling wave.
The existence of travelling wave solutions for certain hyphae growth models has already been proven. However, these models do not take into account the dynamics in the cell wall and consequently have to prescribe explicitly how the wall grows as new material arrives. Our new model overcomes this by modelling the cell wall as a thin viscous sheet where ageing of the cell wall results in hardening of the wall. Our numerical study indicates that the desired solution exists for the governing ODE. The aim of my current work concerns proving analytically the existence of this solution.
Using continuation methods to find new states in an aggregation model
Most of the well known non-local aggregation models consider individuals with unlimited, unrestricted sensing and also typically only consider a single type of individual. Further they typically only consider forces of attraction and repulsion. [1] A model introduced by Dr. Eftimie breaks these ideas by having potentially restricted sensing, two types of the same species, and the addition of a third social force, alignment. With the simplifications removed, the dynamics that can be observed are richer than the typical single or double pulse equilibria. [2]
We highlight briefly some of the other unique features of the model then introduce pseudo-arclength continuation to detect other stationary or periodic states. We begin with the constant valued steady state and then vary parameters along with the solution in order to quickly get a state for a given set of parameters. This is more desirable than evolving the equations as they generally take long times to evolve to a stationary state and even then it is questionable whether it is stationary.
The continuation does not yet work though as there are degeneracies in the matrix of the Newton system caused from symmetries in the model, we believe. We make note of some symmetries that exist within the model itself and show the degenerate eigenvectors, giving more evidence that the symmetries cause the degeneracies. We show how to remove some degeneracies like that caused by translational symmetry and end with recent steps forward.
References
- Topaz, C. Bernoff, A. A primer of swarm equilibria. SIAM Journal on Applied Dynamical Systems, 10:212-250, 2011
- Eftimie R. de Vries G. Lewis, M. Complex spatial group patterns result from different animal communication mechanisms. Proceedings of the National Academy of Sciences of the United States of America, 104:6974-6979, 2007

Well-posedness of the Cauchy problem for nonlinear Kolmogorov-Fokker-Planck equations for measures
A preprint of a paper related to the content of this poster is available here.
We study the well-posedness of the following Cauchy problem : \[ \partial_{t}\mu_{t}=\partial_{x_{i}x_{j}}(a^{ij}(x,t,\mu)\mu_{t})-\partial_{x_{i}}(b^{i}(x,t,\mu)\mu_{t}),\quad\mu_{0}=\nu, \] where \(\mu_{t}\) and \(\nu\) are probability measures on \(\mathbb{R}^{d}\).
Sufficient conditions for the existence of local and global-in-time
probability solutions are given. We indicate some conditions under
which global-in-time solutions don't exist. Moreover we show one
possible approach to the study of uniqueness for such problems. In all
cases we admit unbounded coefficients and both degenerate and
nondegenerate diffusion matrices.

BV estimates in optimal transportation and applications
The purpose of this work is to present some recent BV estimates in the theory of optimal transportation. We use this estimations to study a wide range of prob- lems. More precisely we analyse projection and obstacle-like problems in Wasserstein spaces w.r.t. the quadratic cost, where we show that the total variation of the pro- jection of a BV probability density decreases w.r.t. the total variation of the original density. Between others this remarkable property allows us to get compactness prop- erties and quantitative estimates in evolution equations. By the means of our results we can give an elegant proof (relying on optimal transportation) of the decrease in time of the total variation of the solution of the porous medium equation. Moreover it helps us to get some estimates for crowd movements, allowing to prove existence results of a second order macroscopic model with congestion (similar to the ones introduced by Maury, Roudneff-Chupin and Santambrogio, see [3], but inserting some stochastic influence, arriving to a Fokker-Planck type equation, see [2]), which is also motivated by some second order mean field games with density constraints.
This is a joint work with G. De Philippis, F. Santambrogio and B. Velichkov ([1]).
References
- G. De Philippis, A. R. Mészáros, F. Santambrogio, B. Velichkov, BV estimates in optimal transportation with applications, in preparation.
- R. Jordan, D. Kinderlehrer, F. Otto, The variational formulation of the Fokker-Planck equation, SIAM J. Math. Anal., 29 (1998), No. 1, 1-17.
- B. Maury, A. Roudneff-Chupin, F. Santambrogio, A macroscopic crowd motion model of gradient flow type, Math. Models and Meth. in Appl. Sci., 20 (2010), No. 10, 1787-1821.

Discrete-to-continuum limits in plasticity
My 1-dimensional, first order in time, non-locally interacting particle system models plasticity of metals. I show how one can pass to the limit by exploiting that it is a gradient flow of a convex energy.

Dynamics for a system of screw dislocations
We describe the dynamics for a system of screw dislocations subject to anti-plane shear. Variational techniques allow us to find minimizers for the energy functional associated with the system of dislocations in an elastic medium. Building on a model by Cermelli and Gurtin, a weak notion of solutions (in the sense of Filippov) to ordinary differential equations is used to solve the dynamics problem. Some examples of interesting scenarios complement the presentation.
Interacting fibre equations
We present a surrogate model describing the lay-down process of fibres in the production process of non wovens. Those have a variety of applications, for example as filter materials in cars.
In comparison to former results, we include the interaction of the fibres and therefore model the thickness of those by a local interaction potential with delay depending on parameters associated to the radii and other material properties of the fibres.

Time dependent mean-field games
We consider time dependent mean-field games (MFG) with a local power-like dependence on the measure and Hamiltonians satisfying both sub and superquadratic growth conditions. We establish existence of smooth solutions under a certain set of conditions depending both on the growth of the Hamiltonian as well as on the dimension. In the subquadratic case this is done by combining a Gagliardo-Nirenberg type of argument with a new class of polynomial estimates for solutions of the Fokker-Planck equation in terms of \(L^r L^p\)-norms of \(D_pH\). These techniques do not apply to the superquadratic case. In this setting we recur to a delicate argument that combines the non-linear adjoint method with polynomial estimates for solutions of the Fokker-Planck equation in terms of \(L^\infty L^\infty\)-norms of \(D_pH\). Concerning the subquadratic case, we substantially improve and extend the results previously obtained. Furthermore, to the best of our knowledge, the superquadratic case has not been addressed in the literature yet. In fact, it is likely that our estimates may also add to the current understanding of Hamilton-Jacobi equations with superquadratic Hamiltonians. This is a joint work with D. Gomes and H. Sanchez-Morgado.

Kinetic and mean-field modeling of financial markets
The financial crisis of the past years showed that many standard financial market models are unable to explain anomalous events. These anomalous market behaviors which are called stylized facts are universal market properties. They can be observed at stock markets all over the world. Pareto tails in wealth distributions and stock returns are well known examples for such stylized facts.
New econophysical models consider behavioral aspects of agents which are assumed to play an important role in the formation of stylized facts. These systems of many interacting financial agents are simulated by the Monte Carlo method, but the connection between irrational behavior of agents and the formation of stylized facts still needs to be explored.
The goal of this project is to derive kinetic equations from the microscopic agent models. Such a kinetic equation would enable an analysis of the relation between irrational behavior of agents and the appearance of stylized facts. First challenges in this project are the mathematical modeling of irrational agents and especially the correct kinetic limit of the microscopic model.
Socio-economic applications of finite state mean field games
We present some applications of finite state mean field games to socio-economic sciences. Such games are described by a system of hyperbolic PDEs for which we present a new numerical method. We exploit the so called potential mean field games and we illustrate the behavior of solutions that might develop shocks. We finish by analyzing this shock structure in the case of two-state problems.
This is a joint work with D. Gomes and M.-T. Wolfram.
United by noise: randomness helps swarms stay together

Among the most striking aspects of the movement of many animal groups are their sudden coherent changes in direction. Recent observations of locusts and starlings have shown that this directional switching is an intrinsic property of their motion. Similar direction switches are seen in self-propelled particle and other models of group motion. Comprehending the factors that determine such switches is key to understanding the movement of these groups. Here, we adopt a coarse-grained approach to the study of directional switching in two alignment models (one a spatial self-propelled particle model, the other a non-spatial reaction system) assuming an underlying one-dimensional Fokker–Planck equation for the alignment of the particles. We continue with this assumption in analysing experimental data on locusts and use a similar systematic Fokker–Planck equation coefficient estimation approach to extract the relevant information for the assumed Fokker–Planck equation underlying that experimental data. In the experiment itself the motion of groups of 5 to 100 locust nymphs was investigated in a homogeneous laboratory environment, helping us to establish the intrinsic dynamics of locust marching bands. We determine the mean time between direction switches as a function of group density for the experimental data and the self-propelled particle model. This systematic approach allows us to identify key differences between the experimental data and the model, revealing that individual locusts appear to increase the randomness of their movements in response to a loss of alignment by the group. We give a quantitative description of how locusts use noise to maintain swarm alignment. We discuss further how properties of individual animal behaviour, inferred by using the Fokker–Planck equation coefficient estimation approach, can be implemented in the self propelled particle model to replicate qualitatively the group level dynamics seen in the experimental data.

Boltzmann type control of opinion consensus through leaders
An arXiv preprint of a paper related to the content of this poster is available here. There are also movies of the presented numerical simulations at the author's webpage.
(G. Albi, L. Pareschi, M. Zanella)
The study of formations and
dynamics of opinions leading to the so called opinion consensus is one
of the most important areas in mathemati- cal modeling of social
sciences. Following the Boltzmann type control recently introduced in
[1], we consider a group of opinion leaders which modify their
strategy accordingly to an objective functional with the aim to
achieve opinion consensus. The main feature of the Boltzmann type
control is that, thanks to an instantaneous binary control
formulation, it permits to embed the minimization of the cost
functional into the microscopic leaders interactions of the
corresponding Boltzmann equation. The related Fokker-Planck asymptotic
limits are also derived which allow to give explicit expressions of
stationary so- lutions, which are consistent with [2]. Numerical tests
show how this approach explains common sociologial features of
political strategies, such as populism of radical parties and the
minimum differentiation principle, also known in Game Theory as
Hotelling’s linear city model. The results demonstrate the validity of
the Boltzmann type control approach and the capability of the leaders
control to strategically lead the followers opinion.
References
- Giacomo Albi, Michael Herty, and Lorenzo Pareschi. Kinetic description of optimal control problems and applications to opinion consensus. To appear on Comm. Math. Sci., 2014.
- Bertram Düring, Peter Markowich, Jan-Frederik Pietschmann, and Marie-Therese Wolfram. Boltzmann and Fokker-Planck equations modelling opinion formation in the presence of strong leaders. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Science, 465(2112):3687–3708, 2009.
Coalescing diffusion in the Keller-Segel model
One of the primary models for describing chemotactic aggregation is the Keller-Segel model. It is known that this model can exhibit the formation of singularities in finite time, past which the the system cannot be propagated. Under some assumptions, it's possible to derive exact conditions for the formation of these blow-ups. We take advantage of this fact to introduce an interacting particle-based regularization of this system, in which the formation of singularities corresponds to the the coalescence of particle aggregates into massive particles of low variance. We investigate the analytical aspects of this interacting particle systems, and present a numerical implementation which allows us to investigate the K-S system in the plane.


